The Law of Benford!

Benford’s Law is an intriguing phenomenon that I heard of in the past and always wanted to check it out for myself. This mathematical law has many applications, probably most well known to be used in Fraud Detection.
Imagine you have a large list of numbers, whether it is your own personal bank transactions, stock prices, bills, street addresses, mathematical constants, population counts, etc… you name it. Now, consider the leading digits for those numbers, which will be one of these digits: 1, 2, 3, 4, 5, 6, 7, 8, or 9. Which digit would you bet on if you were to choose only one? You might imagine the distribution of these leading digits are equal, with ~11.11% chance for each digit. Turns out, this assumption is incorrect, and we will use real data to see for ourselves!
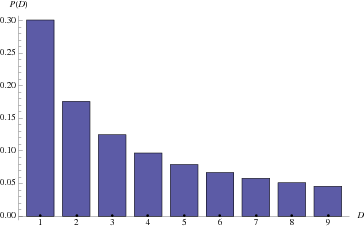
Essentially, this is a mathematical law that describes frequency distribution of leading digits in many real-life numeric data. You can read more about Benford’s Law from its Wikipedia article.
I was reminded of Benford’s Law after listening to a Linear Digressions podcast. (I love this podcast by the way, I highly recommend it! Especially if you are interested in Data Science)
We will acquire some data from the web, including Yahoo Finance; perform some quick transformations; and investigate the distributions by a histogram. Head over to my iPython Notebook found on GitHub:
My ipython notebook here: benford.ipynb

Cowboys of the Law.

